Dzisiaj część druga poznawania programu SMath Studio.
Jest to darmowy program komputerowy (freeware), który pomoże nam przeprowadzić obliczenia matematyczne a także narysować wykresy.
Korzystając z funkcji programy policzymy sobie natężenie pola grawitacyjnego wokół Ziemi, oraz sprawdzimy jak zachowuje się grawitacja pomiędzy Ziemią a Księżycem. Zachęcam do lektury i samodzielnej pracy.
Wartość siły grawitacji możemy obliczyć ze wzoru:
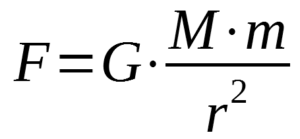
F – wartość siły grawitacji
G — stała grawitacji
M – masa Ziemi
m – masa ciała na które działa grawitacja
Dla nas wygodniej będzie się jednak posługiwać natężeniem pola grawitacyjnego.
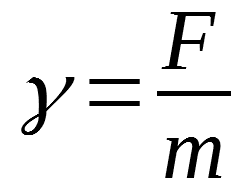
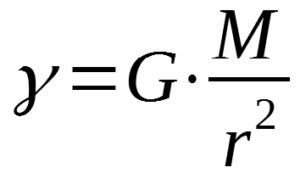
Zobaczmy jak wygląda wartość natężenia pola grawitacyjnego wokół Ziemi.
Na początek otwórzmy program SMath i zadeklarujmy potrzebne nam wartości: masę oraz promień Ziemi.

Następnie proponuję opisać nasze dane. Klikamy prawym klawiszem myszy i wybieramy
„Pokaż opis”. Uzupełniamy pole które się pojawiło.
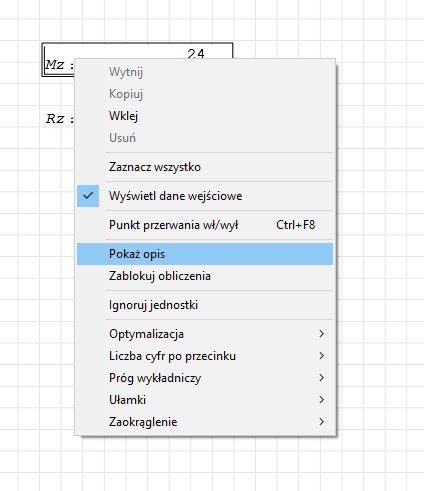

Następnie korzystając z wcześniej podanego wzoru utwórzmy funkcję γ®
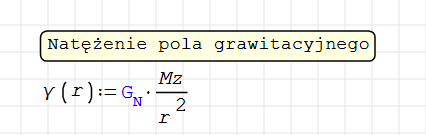
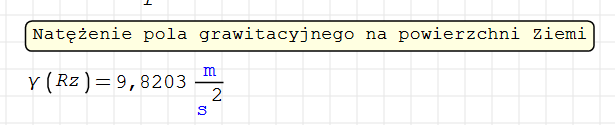
Sprawdźmy jaką wartość przyjmuje natężenie pola grawitacyjnego na powierzchni Ziemi.
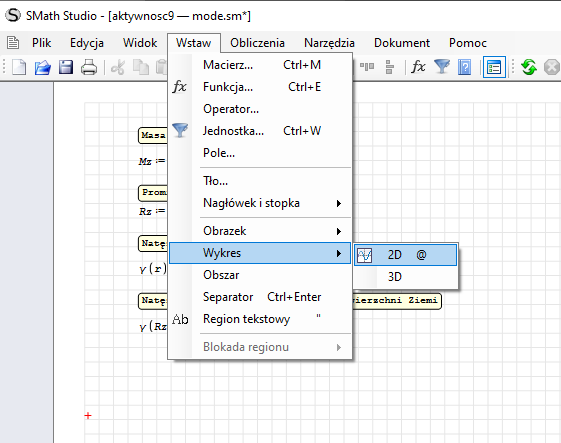
Wstawmy wykres, z menu „wstaw” wybieramy wykres→2D
Rozciągamy wykres wciskając lewy przycisk mysz na kropce w prawym dolnym rogu
W lewym dolnym rogu wpisujemy naszą funkcję ( UWAGA! Jako argument podajemy x).
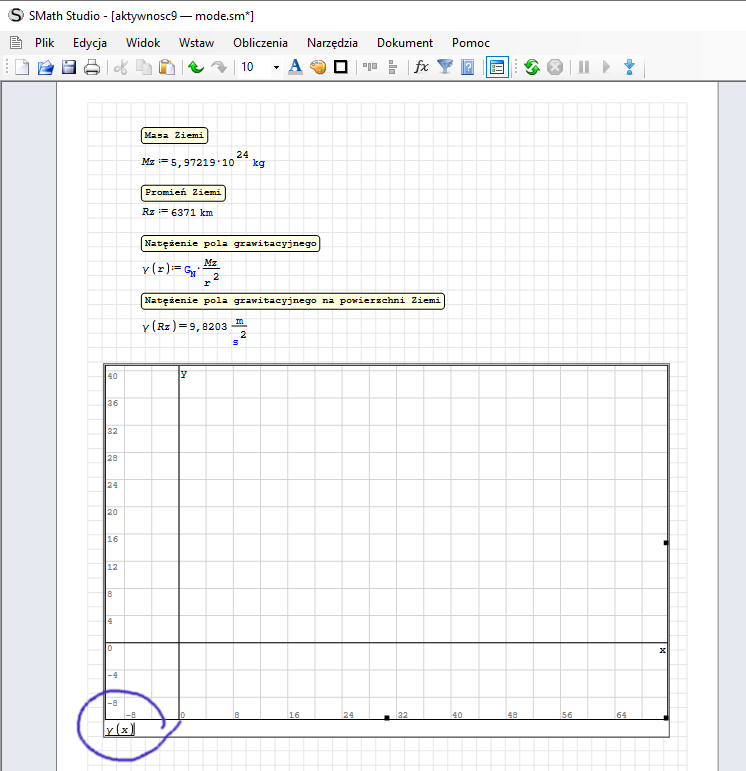
Kilka słów o nawigacji:
• wciskając lewy przycisk myszy na wykresie możemy przesuwać obszar widziany w oknie
• korzystając z rolki skalujemy wykres w obu osiach jednakowo
• wciskając klawisz „SHIFT” i przewijając rolkę myszki skalujemy oś „x”
• wciskając klawisz „Ctrl” i przewijając rolkę myszki skalujemy oś „y”
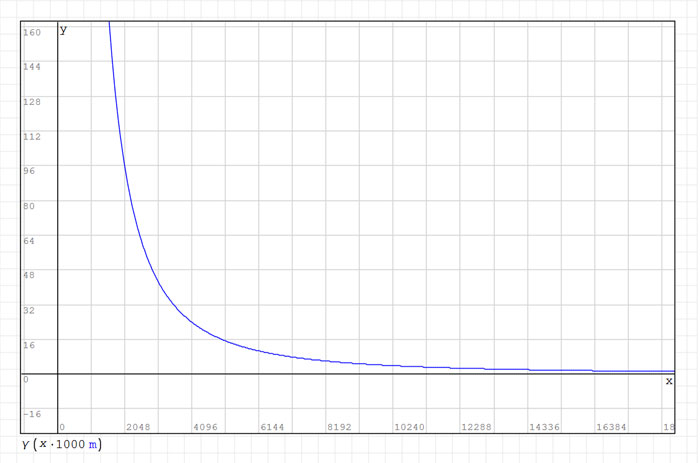
Niestety w tym momencie na wykresie nie widać wykresu naszej funkcji. Nasza oś x obejmuje wartości od zera do kilkudziesięciu a przecież sam promień Ziemi to ponad 6000 kilometrów.
Dodatkowo należy pamiętać, że wykres tworzony jest w jednostkach podstawowych, więc oś x jest wyrażona w metrach. Aby temu zaradzić proponuję zamienić γ(x) na γ(x * 1000 m).
Uzyskamy w ten sposób oś x wyrażoną w kilometrach, co ułatwi odbiór wykresu. Dodanie jednostki jest ważne, gdyż w niektórych przypadkach jej brak może spowodować problemy z otrzymaniem wyniku.
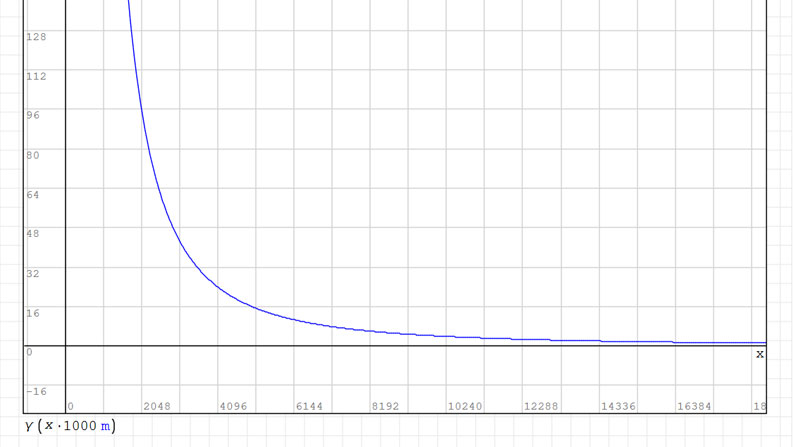
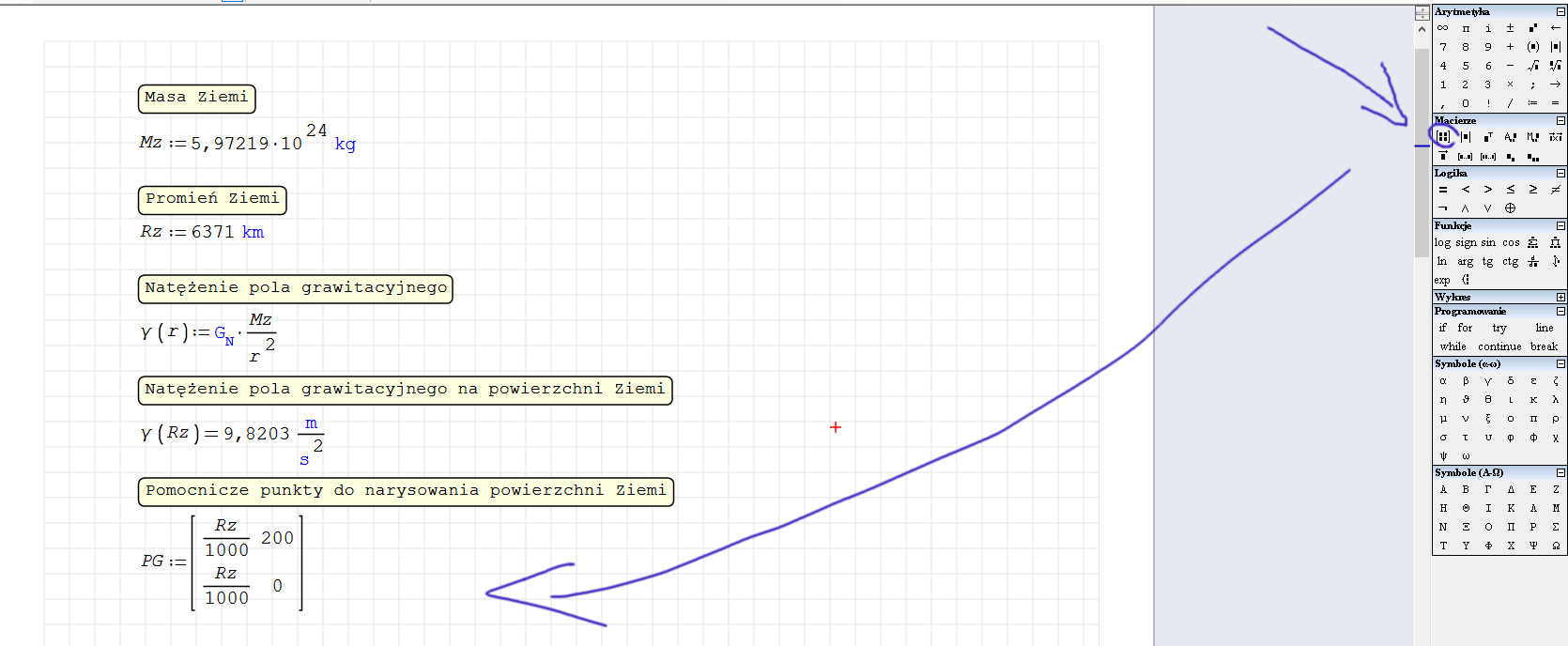
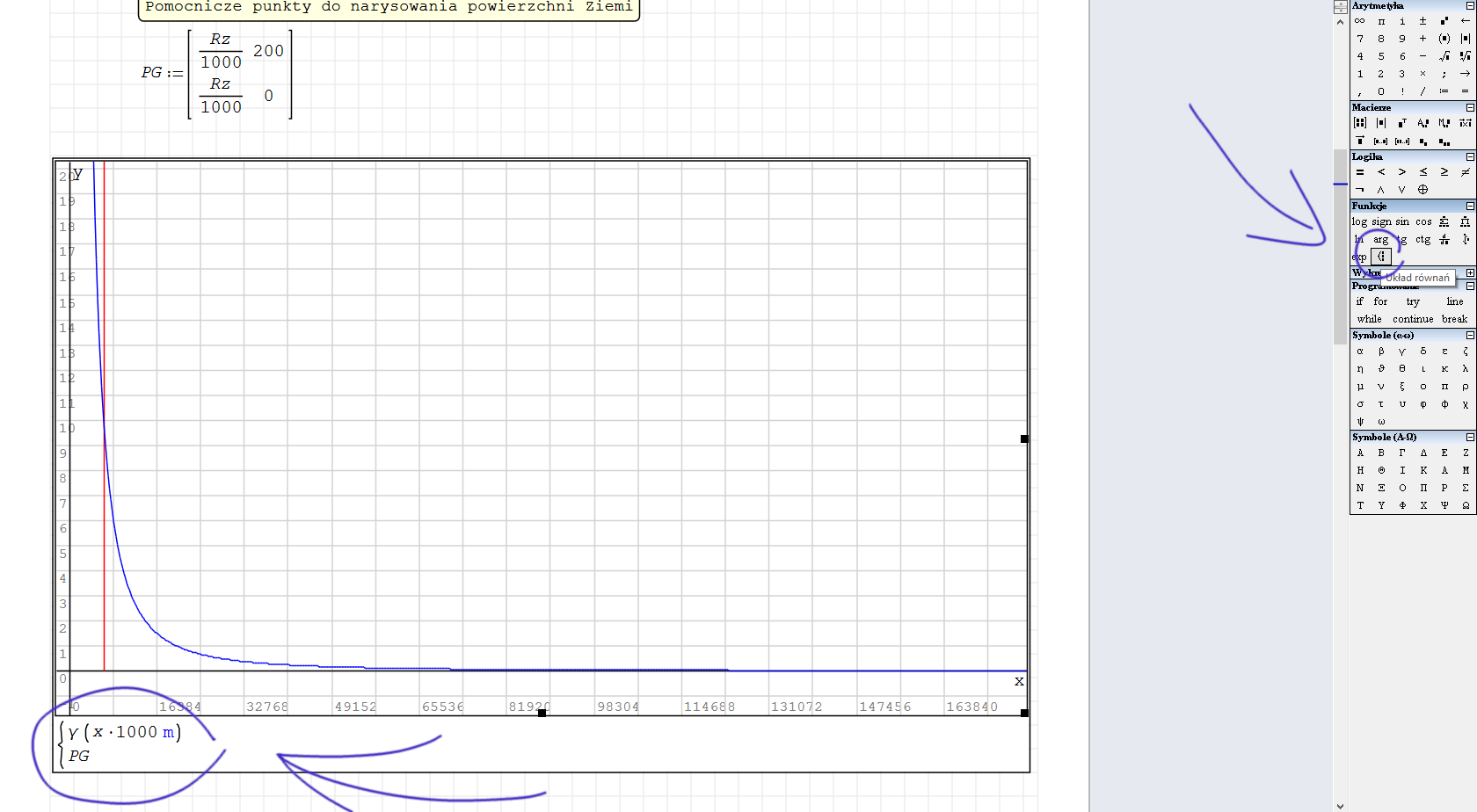
Wzór na natężenie pola grawitacyjnego nie jest prawdziwy wewnątrz ciała. Warto więc oznaczyć na wykresie promień Ziemi. Aby to zrobić musimy dodać pionową linie. Można to zrobić dodając macierz której elementy są współrzędnymi początku i końca linii.
Jako pierwszą współrzędna początku linii wpisujemy promień Ziemi (pamiętamy, że program operuje na metrach a wykres mamy w km, więc dzielimy przez 1000), jako drugą podajemy wysokość linii (200). Analogicznie postępujemy z końcem linii. Ponieważ linia ma być pionowa pierwsza współrzędna się nie zmienia, druga to zero.
Aby na wykresie umieścić więcej niż jedną funkcję, należy najpierw wybrać przycisk „układ równań”. Pozwoli nam to dodać oprócz wykresu funkcji, linię narysowaną na podstawie punktów z macierzy.
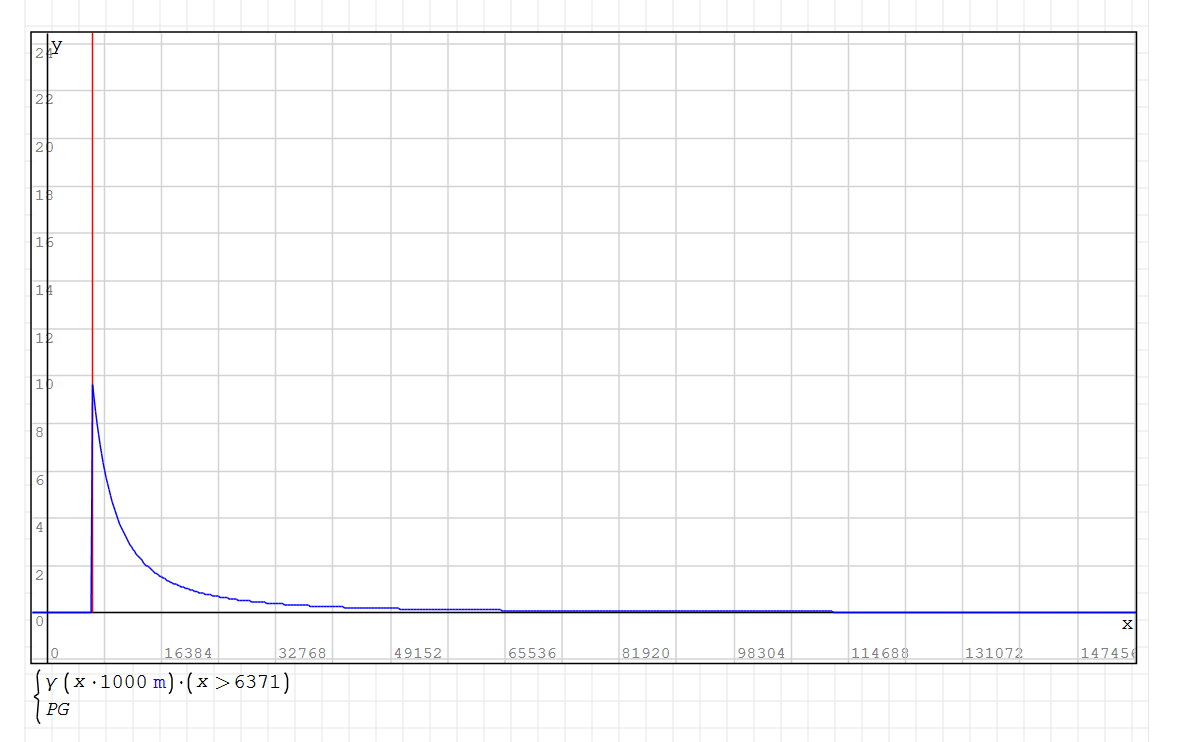
Można także ograniczyć wykres podając po znaku możenia w nawiasie warunek logiczny (x>6371).
W taki oto sposób otrzymaliśmy wykres natężenie pola grawitacyjnego na przykładzie Ziemi.
Zastanówmy się jak wyglądałby taki wykres dla dwóch ciał np. Ziemi i Księżyca. (pomijamy wszystkie inne siły oraz wpływ pozostałych ciał Układu Słonecznego).
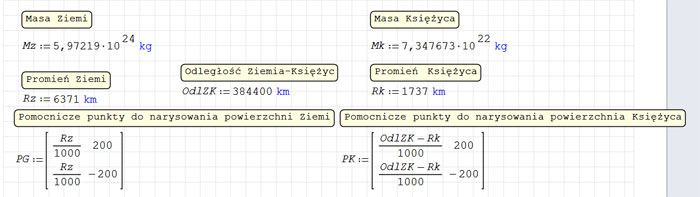
Podobnie jak wcześniej definiujemy potrzebne dane.
Wartość natężenia pola grawitacyjnego dla ciała znajdującego się pomiędzy Ziemią a Księżycem opisuje wzór:
Mz – masa Ziemi
Mk – masa Księżyca
OdlZK – odległość Ziemia-Księżyc
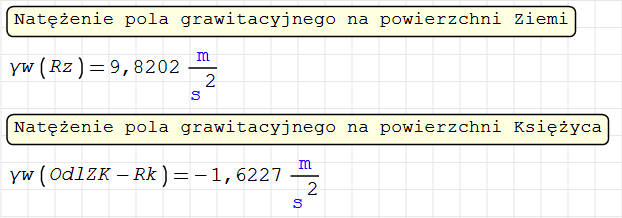
Wstawiając odpowiednie odległości (oś x zaczyna się w środku Ziemi) obliczamy wartość
natężenia pola grawitacyjnego na Ziemi i na Księżycu. Wynik uzyskany dla Księżyca jest ujemny ponieważ natężenia pola grawitacyjnego ma przeciwny zwrot w stosunku do osi x.
Spróbujmy policzyć, czy występują miejsca w których natężenia pola grawitacyjnego ma wartość zero. Użyjemy do tego funkcji solve. Przyjmuje ona 2 lub 4 parametry. Pierwszy to nasza funkcja, drugi to zmienna dla której będziemy poszukiwać miejsc zerowych. Opcjonalnie można podać dwa dodatkowe parametry, a jest to przedział w którym będziemy poszukiwać miejsc zerowych.
Funkcja ta ma jednak istotne ograniczenie. Działa maksymalnie w zakresie od ‑1000 do + 1000 dla wskazanej zmiennej (standardowe ustawienia to ‑20 +20 można to zmienić w Narzędzia → Ustawienia, zakładka „Obliczenia”, pole „Pierwiastki zakres”).
Aby obejść ten problem trzeba przeskalować funkcję do wskazanego zakresu. Dlatego zamiast γw(x) pojawia się γw(x*106). Uzyskany wynik trzeba ponownie pomnożyć przez 106.
Wyliczona wartość nie pokrywa się z punktem Lagrange’a L1 ponieważ zaniedbane zostały pozostałe siły.
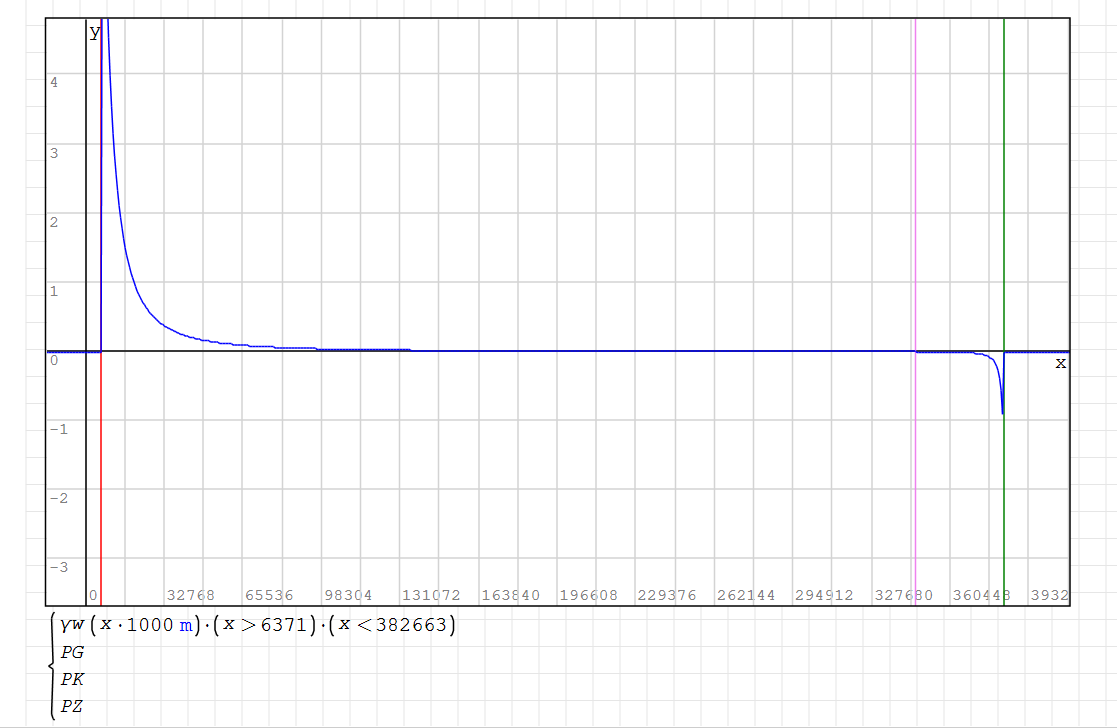
Korzystając z uzyskanych danych rysujemy wykres:
Tak jak poprzednio zachęcam do dalszego poznawania zalet i ograniczeń programu SMath Studio.
Łukasz Maślaniec


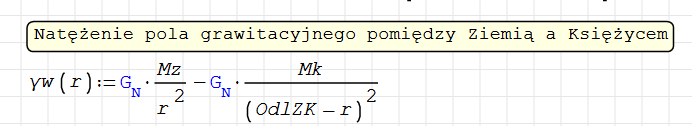
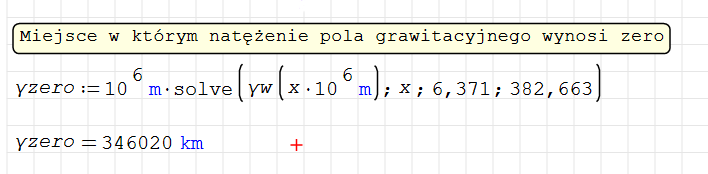
0 komentarzy