Mate­ma­ty­ka bez liczenia

 

Jeże­li mate­ma­ty­ka koja­rzy Ci się tyl­ko z nie­koń­czą­cy­mi się obli­cze­nia­mi, to ta pro­po­zy­cja pozwo­li Ci zupeł­nie ina­czej spoj­rzeć na kró­lo­wą nauk. Dzi­siaj zabio­rę Cię do świa­ta mate­ma­ty­ki, w któ­rym nie poja­wi się ani jed­no dzia­ła­nie, za to będzie dużo dobrej zaba­wy. Naj­pierw poeks­pe­ry­men­tu­je­my z pew­ną wyjąt­ko­wą wstę­gą, a następ­nie zaj­mie­my się sta­ro­żyt­ną chiń­ską łami­głów­ką, któ­ra wcią­ga na dłu­gie godziny.

 

Wstę­ga Möbiusa

Żyją­cy w XIX wie­ku nie­miec­ki mate­ma­tyk i astro­nom, August Möbius, dokład­nie opi­sał fascy­nu­ją­cą figu­rę geo­me­trycz­ną, któ­rą nazy­wa­my wstę­gą Möbiu­sa. Cóż nie­zwy­kłe­go może być w tej figu­rze? Wyko­naj wła­sną wstę­gę i się przekonaj!

Przy­go­tuj:

• kart­kę roz­mia­ru A4
• nożycz­ki
• klej
• pisak

Wyko­na­my dwie wstę­gi, aby porów­nać ich wła­sno­ści: jed­ną nazwie­my zwy­czaj­ną wstę­gą, a dru­gą wstę­gą Möbiusa.
W tym celu wytnij wzdłuż dłuż­sze­go boku kart­ki dwa paski o sze­ro­ko­ści 3 cm. Sklej koń­ce jed­ne­go z pasków. Uzy­ska­łeś zwy­czaj­ną wstęgę.
Weź dru­gi pasek. Jed­ną koń­ców­kę paska obróć o 180° i sklej oba koń­ce. Uzy­ska­łeś wstę­gę Möbiu­sa.

 

 

Na pierw­szy rzut oka wstę­ga Möbiu­sa nie spra­wia wra­że­nia wyjąt­ko­wej figu­ry, jest podob­na do zwy­kłej wstę­gi, tyl­ko bar­dziej skrę­co­na. Zaraz prze­ko­nasz się, jak bar­dzo myl­ne bywa pierw­sze wrażenie.

Ile stron ma zwy­kła wstę­ga? Cóż, odpo­wiedź na to pyta­nie wyda­je się być oczy­wi­sta, wstę­ga ma dwie stro­ny. Aby się upew­nić, że tak jest, nary­suj krop­kę po jed­nej stro­nie wstę­gi. Teraz, bez odry­wa­nia pisa­ka od wstę­gi, nary­suj linię roz­po­czy­na­ją­cą się na nary­so­wa­nej krop­ce. Rysuj, aż znów doje­dziesz pisa­kiem do kropki.

 

 

W efek­cie otrzy­ma­łeś potwier­dze­nie przy­pusz­czeń. Teraz widać wyraź­nie, że ta wstę­ga ma dwie stro­ny: jed­ną pustą, a dru­gą z zazna­czo­ną linią. A ile stron ma wstę­ga Möbiu­sa? Aby się prze­ko­nać powtórz opi­sa­ne powy­żej czyn­no­ści. Pamię­taj, aby nie odry­wać pisa­ka od papieru.

 

 

Nie odry­wa­łeś pisa­ka, nie zmie­nia­łeś stro­ny, po któ­rej pisa­łeś, a mimo to linia jest nary­so­wa­na wzdłuż całej wstę­gi. Nie ma podzia­łu na dwie stro­ny. Wnio­sek jest nastę­pu­ją­cy: wstę­ga Möbiu­sa ma tyl­ko jed­ną stronę!

Ustal­my teraz, ile kra­wę­dzi mają obie wstę­gi. Przyj­rzyj­my się naj­pierw nor­mal­nej wstę­dze. Wybierz jed­ną kra­wędź i prze­suń po niej pisa­kiem, aż dotrzesz do miej­sca, w któ­rym zaczą­łeś (bez odry­wa­nia pisaka).

 

 

Mamy teraz pew­ność, że zwy­kła wstę­ga ma dwie kra­wę­dzie: jed­ną kolo­ro­wą i jed­ną bia­łą. Powtórz czyn­no­ści ze wstę­gą Möbiu­sa, by usta­lić ile ma krawędzi.

 

 

Oka­zu­je się, że wstę­ga Möbiu­sa ma tyl­ko jed­ną krawędź!

To nie koniec zaska­ku­ją­cych wła­sno­ści wstę­gi Möbiu­sa. Sprawdź­my, co się sta­nie, gdy ją prze­tnie­my. Na począ­tek weź zwy­kłą wstę­gę i prze­tnij ją wzdłuż, mniej wię­cej w poło­wie wysokości.

 

Otrzy­ma­li­śmy w ten spo­sób dwie zwy­kłe wstę­gi. Czy moż­na „roz­mno­żyć” wstę­gę Möbiu­sa poprzez ana­lo­gicz­ne postę­po­wa­nie? Sprawdź.

 

 

Prze­cię­cie wstę­gi Möbiu­sa wca­le nie spo­wo­do­wa­ło podzia­łu na dwie wstę­gi. Uzy­ska­li­śmy za to jed­ną więk­szą wstę­gę. Zachę­cam, abyś spraw­dził, czy nadal jest to wstę­ga Möbiu­sa? Ile ma stron? Ile ma krawędzi?

A co, jeże­li prze­tnie­my wstę­gę, ale nie w poło­wie wyso­ko­ści? Wytnij z kart­ki kolej­ny pasek o sze­ro­ko­ści 3 cm. Z jed­nej stro­ny paska nary­suj linię pro­stą w odle­gło­ści 1 cm od kra­wę­dzi, zaś z dru­giej stro­ny nary­suj linię w odle­gło­ści 1cm od dru­giej kra­wę­dzi. Sklej koń­ce przy­go­to­wa­ne­go paska tak, aby uzy­skać wstę­gę Möbiusa.

 

 

Prze­tnij wstę­gę wzdłuż nary­so­wa­nej linii.

 

 

Tym razem, w wyni­ku prze­cię­cia wstę­gi Möbiu­sa, otrzy­ma­li­śmy dwie wstę­gi, na doda­tek połą­czo­ne jak ogni­wa łań­cu­cha. Co cie­ka­we, jed­na z nich jest wciąż wstę­gą Möbiu­sa. Sprawdź, która.

Jak widzisz, wstę­ga Möbiu­sa to wyjąt­ko­wa figu­ra: ma tyl­ko jed­ną stro­nę, jed­ną kra­wędź, a po jej prze­cię­ciu moż­na uzy­skać zaska­ku­ją­ce efek­ty. Być może wyda­je Ci się, że to tyl­ko taka mate­ma­tycz­na cie­ka­wost­ka. Jed­nak wstę­ga Möbiu­sa nie słu­ży jedy­nie do zaba­wy. Opi­sem takich figur zaj­mu­je się jeden z naj­waż­niej­szych dzia­łów współ­cze­snej mate­ma­ty­ki, nazy­wa­ny topo­lo­gią. War­to tutaj wspo­mnieć, że Nagro­da Nobla z fizy­ki w 2016 roku zosta­ła przy­zna­na „za teo­re­tycz­ne odkry­cia w dzie­dzi­nie topo­lo­gicz­nych przejść fazo­wych i topo­lo­gicz­nych faz mate­rii”. Więc, jak widzisz, topo­lo­gia to poważ­na nauka.

Jak się oka­zu­je, wstę­ga Möbiu­sa ma rów­nież wie­le bar­dziej przy­ziem­nych zasto­so­wań. Mod­ne sza­li­ki ład­nie ukła­da­ją się na szyi, ponie­waż są uszy­te wła­śnie na kształt wstę­gi Möbiu­sa. Rów­nież meda­le zawie­sza­ne są na takich tasiem­kach, któ­re są wstę­ga­mi Möbiu­sa, by dobrze się pre­zen­to­wa­ły na zwy­cięz­cach.
W tech­ni­ce uży­wa się taśmo­cią­gów skrę­co­nych w kształt wstę­gi Möbiu­sa, co powo­du­je, że cała powierzch­nia zuży­wa się jed­na­ko­wo. Gdy­by sto­so­wa­no zwy­kłą wstę­gę, to jed­na stro­na była­by eks­plo­ato­wa­na, a dru­ga nie­uży­wa­na, przez co taśma nisz­czy­ła­by się dwa razy szyb­ciej. Wstę­ga Möbiu­sa jest rów­nież sym­bo­lem recyklingu.

Zda­rza się, że two­rzy się książ­ki w kształ­cie wstę­gi Möbiu­sa. Tak zapi­sa­ne histo­rie nigdy się nie koń­czą i moż­na je czy­tać w nie­skoń­czo­ność. Ty rów­nież możesz przy­go­to­wać sobie taką zaska­ku­ją­cą „książ­kę”. W tym celu wydru­kuj plik [PDF].

Wytnij pro­sto­kąt. Zegnij go wzdłuż środ­ko­wej linii i sklej ze sobą obie połów­ki, tak aby powstał pasek zapi­sa­ny z dwóch stron. Nanieś klej na sza­re obsza­ry. Sklej sza­re koń­ce ze sobą. Two­ja nie­koń­czą­ca się histo­ria jest gotowa!

 

 

 

Tan­gram

Tan­gram to zna­na od kil­ku tysię­cy lat ukła­dan­ka wymy­ślo­na przez Chiń­czy­ków. Powsta­je przez podział kwa­dra­tu na mniej­sze figu­ry: dwa duże trój­ką­ty pro­sto­kąt­ne, dwa małe trój­ką­ty pro­sto­kąt­ne, śred­ni trój­kąt pro­sto­kąt­ny, mały kwa­drat i rów­no­le­gło­bok. Z tych zale­d­wie sied­miu ele­men­tów moż­na uło­żyć tysią­ce kształ­tów. Jest to świet­ny tre­ning dla mózgu, roz­wi­ja­ją­cy wyobraź­nię prze­strzen­ną, a jed­no­cze­śnie wcią­ga­ją­ca zaba­wa dla całej rodzi­ny. Aby przy­go­to­wać tan­gram, nale­ży wydru­ko­wać plik [PDF] i postę­po­wać zgod­nie z poniż­szy­mi instrukcjami.

 

Instruk­cja — wer­sja dla leniuszków

Potrze­bu­jesz:

• wydru­ko­wa­ny tangram
• nożycz­ki

 

 

Wytnij wszyst­kie ele­men­ty wzdłuż nary­so­wa­nych linii. I gotowe!

 

 

Nie­ste­ty teraz Two­ja ukła­dan­ka nie jest zbyt wytrzy­ma­ła ani atrak­cyj­na wizu­al­nie. Dodat­ko­wo, nawet wzię­cie głęb­sze­go odde­chu może spo­wo­do­wać prze­su­nię­cie uło­żo­nych ele­men­tów, co budzi nie­ma­łą iry­ta­cję. Jeśli chcesz przy­go­to­wać ład­ny tan­gram, któ­ry dłu­go Ci posłu­ży, sko­rzy­staj z dru­giej wer­sji instrukcji.

 

Instruk­cja — wer­sja dla ambitnych

Potrze­bu­jesz:

• wydru­ko­wa­ny tangram
• nożycz­ki
• kawa­łek tek­tu­ry (u mnie jest to ostat­nia stro­na z blo­ku, spraw­dzi się też okład­ka ze sta­re­go zeszytu)
• klej
• kart­ka
• kred­ki lub pisaki
• taśma kle­ją­ca

 

 

Krok 1
Przy­go­tuj wydruk i nożycz­ki. Wytnij cały kwa­drat, bez wyci­na­nia poszcze­gól­nych elementów.

 

 

Krok 2
Dokład­nie nanieś klej na dru­gą (nie zadru­ko­wa­ną) stro­nę kwadratu.

 

 

Krok 3
Przy­klej tan­gram do tektury.

 

 

Krok 4
Wytnij tek­tu­rę tak, aby mia­ła roz­miar przy­kle­jo­ne­go kwadratu.

 

 

Krok 5
Dokład­nie nanieś klej na dru­gą stro­nę tek­tu­ry i przy­klej do kart­ki. Następ­nie wytnij kart­kę tak, by mia­ła roz­miar przy­kle­jo­nej tektury.

 

 

Jeże­li Two­ja tek­tur­ka ma kolor bia­ły i da się po niej ryso­wać kred­ka­mi lub pisa­ka­mi, to możesz pomi­nąć ten krok. Moja tek­tur­ka jest brzyd­ka, dla­te­go zasło­ni­łam ją kratką.

 

Krok 6
Gdy wszyst­kie war­stwy są do sie­bie przy­kle­jo­ne, możesz wyciąć poszcze­gól­ne ele­men­ty ukła­dan­ki wzdłuż wydru­ko­wa­nych linii.

 

 

Krok 7
Poko­lo­ruj ele­men­ty z obu stron.

 

 

Krok 8
Aby figu­ry zbyt szyb­ko się nie znisz­czy­ły oraz nie roz­kle­iły, oklej je taśmą kle­ją­cą. Tak zabez­pie­czo­ne ele­men­ty powin­ny wytrzy­mać wie­le godzin zaba­wy, a byle mach­nię­cie dło­nią nie zdmuch­nie ich ze stołu.

 

 

Zasa­dy gry

W zaba­wie cho­dzi o to, by uło­żyć obra­zek na pod­sta­wie poda­ne­go wzor­ca. Moż­na rów­nież ukła­dać obraz­ki według wła­snej wyobraź­ni. W obu przy­pad­kach obo­wią­zu­ją nastę­pu­ją­ce reguły:

• nale­ży użyć wszyst­kich elementów
• ele­men­ty powin­ny się stykać
• ele­men­ty nie mogą na sie­bie nachodzić
• ele­men­ty moż­na dowol­nie odwracać

Przy­kład:

 

 

Roz­grzew­ka

Na począ­tek ułóż wzór poda­ny poni­żej. Wszyst­kie linie są zazna­czo­ne, abyś mógł w łatwy spo­sób potre­no­wać układanie.

 

 

 

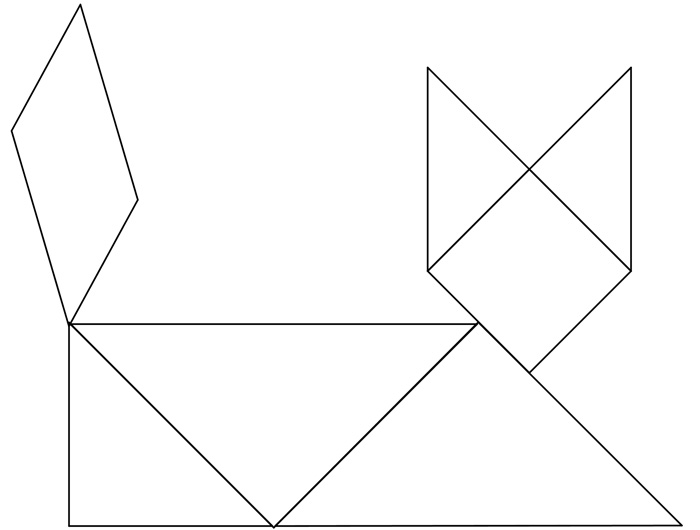
Przy­kła­do­we wzory
Czas na coś trud­niej­sze­go! Poni­żej przed­sta­wio­ne są wzo­ry obraz­ków do uło­że­nia. Tym razem musisz samo­dziel­nie zde­cy­do­wać, gdzie i jak dany ele­ment powi­nien być uło­żo­ny. Jeśli nie będziesz mógł sobie pora­dzić z któ­rymś przy­kła­dam, zaproś do zaba­wy rodzi­nę lub przy­ja­ciół. Ukła­da­nie takich obraz­ków to cie­ka­we wyzwa­nie, któ­re wcią­ga i małych, i dużych.

 

 

 

 

 

 

 

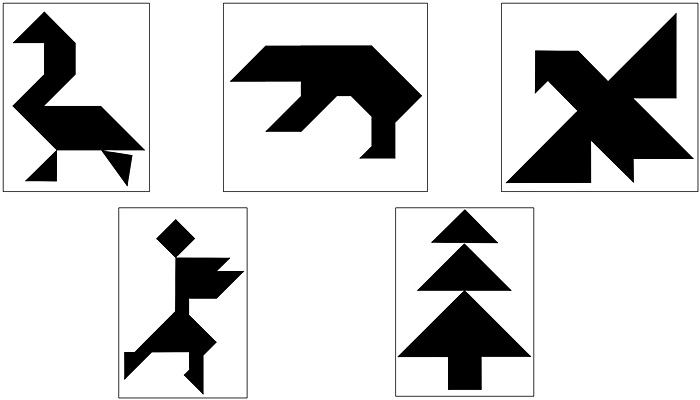
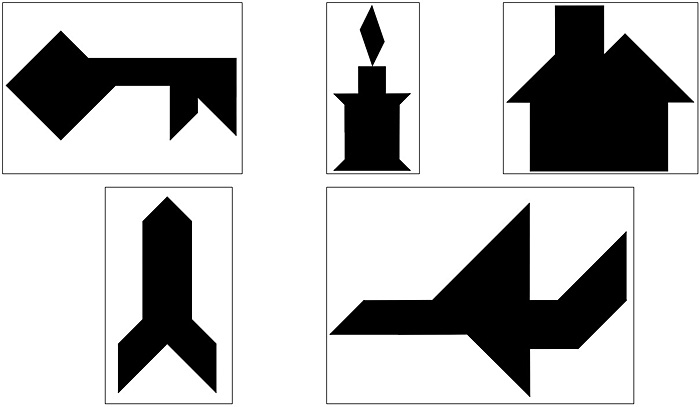
Jeśli uda­ło Ci się już odwzo­ro­wać wszyst­kie zapro­po­no­wa­ne obraz­ki, to nad­szedł czas, abyś wymy­ślił swo­je wła­sne kształty 🙂

Powo­dze­nia!

 

Alek­san­dra Kowalska