Sza­co­wa­nie licz­by Pi

 

Data czter­na­ste­go mar­ca zapi­sa­na w ame­ry­kań­skim for­ma­cie 3.14 koja­rzy się z licz­bą π, dla­te­go wła­śnie tego dnia obcho­dzo­ny jest dzień licz­by π. Z tej oka­zji przyj­rzy­my się dzi­siaj bli­żej jed­nej z naj­słyn­niej­szych liczb i spró­bu­je­my wyzna­czyć jej war­tość za pomo­cą… wykałaczek.

LICZBA PI
Jeśli doko­na­my dzie­le­nia dłu­go­ści obwo­du koła (lub okrę­gu) i dłu­go­ści jego śred­ni­cy, to w wyni­ku otrzy­ma­my jed­ną z naj­słyn­niej­szych sta­łych mate­ma­tycz­nych- licz­bę π. Nie ma zna­cze­nia, czy roz­wa­żać będzie­my małe, czy duże koła- wynik takie­go dzie­le­nia zawsze da tę samą liczbę.

 

 

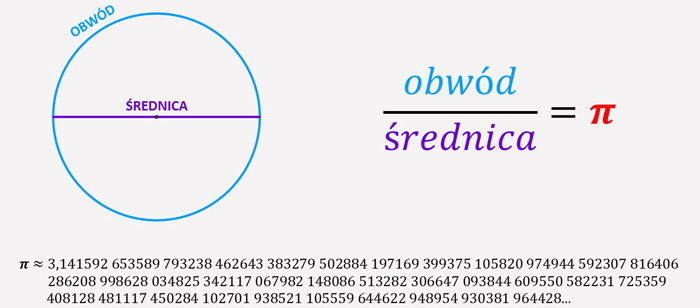
π to licz­ba nie­wy­mier­na, co ozna­cza, że posia­da nie­skoń­czo­ne nie­okre­so­we roz­wi­nię­cie dzie­sięt­ne. Mówiąc języ­kiem mniej nauko­wym: chcąc okre­ślić dokład­nie war­tość licz­by π, nale­ża­ło­by podać nie­skoń­cze­nie wie­le cyfr po prze­cin­ku. Dla­te­go w prak­ty­ce naj­czę­ściej korzy­sta się z przy­bli­żo­nej war­to­ści 3,14. Cza­sem, wyko­nu­jąc pre­cy­zyj­niej­sze obli­cze­nia, przyj­mu­je się, że π wyno­si 3,14159.

Ludzie od sta­ro­żyt­no­ści sta­ra­li się wyzna­czyć przy­bli­żo­ną war­tość licz­by π. Na począt­ku przyj­mo­wa­no, że π jest rów­ne 3. Z bie­giem cza­su wyzna­cza­no coraz lep­sze przy­bli­że­nia. Rekor­dzi­stą w „ręcz­nym” obli­cza­niu kolej­nych war­to­ści po prze­cin­ku licz­by π jest Wil­liam Shanks. W 1874 roku podał licz­bę π z 707 miej­sca­mi po prze­cin­ku. Obli­cze­nia zaję­ły mu 15 lat. Nie­ste­ty, oka­za­ło się, że 180 ostat­nich cyfr wyzna­czył błędnie.
Dziś, oczy­wi­ście, nikt takich obli­czeń nie wyko­nu­je na kart­ce. W 2020 roku za pomo­cą kom­pu­te­ra wyzna­czo­na 50 bilio­nów (!) miejsc po prze­cin­ku licz­by π. Obli­cze­nia trwa­ły 303 dni. Ty rów­nież możesz spró­bo­wać wyzna­czyć war­tość licz­by π. Nie będziesz do tego celu potrze­bo­wał kom­pu­te­ra. Wystar­czy Ci wykałaczka!

 

PI UKRYTE W GRZE HAZARDOWEJ
W XVIII wie­ku popu­lar­no­ścią cie­szy­ła się pew­na gra hazar­do­wa. Pole­ga­ła na rzu­ca­niu igły na plan­szę z nary­so­wa­ny­mi rów­no­le­gły­mi linia­mi. Oso­by bio­rą­ce udział w grze zakła­da­ły się, czy igła po rzu­cie będzie prze­ci­na­ła któ­rąś z linii.

 

 

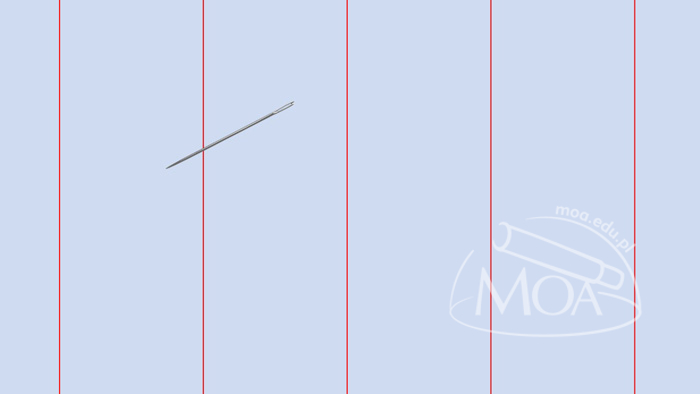
Obser­wu­jąc prze­bieg gry, moż­na było zauwa­żyć, że jeśli odle­głość mię­dzy linia­mi jest rów­na dłu­go­ści igły, to szan­sa na to, że igła będzie prze­ci­nać linię jest więk­sza niż szan­sa na to, że igła nie będzie prze­ci­nać linii. Tema­tem tym zain­te­re­so­wał się fran­cu­ski mate­ma­ty­ki Geo­r­ges Buf­fon. Obli­czył on, że praw­do­po­do­bień­stwo, że igła rzu­co­na loso­wo na plan­szę będzie prze­ci­nać któ­rąś z linii wyno­si 2/π. Mate­ma­ty­ka potra­fi zaska­ki­wać- w spo­sób nie­spo­dzie­wa­ny licz­ba π, koja­rzą­ca się raczej z geo­me­trią i okrę­ga­mi, poja­wi­ła się w ana­li­zie szans na wygra­ną w grze hazar­do­wej. Meto­da wyzna­cza­nia licz­by π, któ­rą za chwi­lę poznasz, nazy­wa się wła­śnie meto­dą Buffona.

 

WYZNACZ SOBIE LICZBĘ PI

Przy­go­tuj:

• Kart­kę roz­mia­ru A3
• Linij­kę
• Ołówek/ pisak
• 20 jed­na­ko­wych patycz­ków np. wyka­ła­czek, zapa­łek, patycz­ków higienicznych
• Potrzeb­na będzie rów­nież kart­ka do zapi­sy­wa­nia wyni­ków, możesz sko­rzy­stać z przy­go­to­wa­nej tabeli

 

 

KROK 1
Zmierz dłu­gość patyczka.

 

 

KROK 2
Nary­suj na kart­ce rów­no­le­głe linie w odstę­pach rów­nych dłu­go­ści patyczka.

 

 

KROK 3
Rzuć w spo­sób loso­wy wyka­łacz­ki na kartkę.

 

 

Policz, ile z rzu­co­nych patycz­ków prze­ci­na któ­rą­kol­wiek z linii.

 

 

Zapisz wynik.

 

 

KROK 4
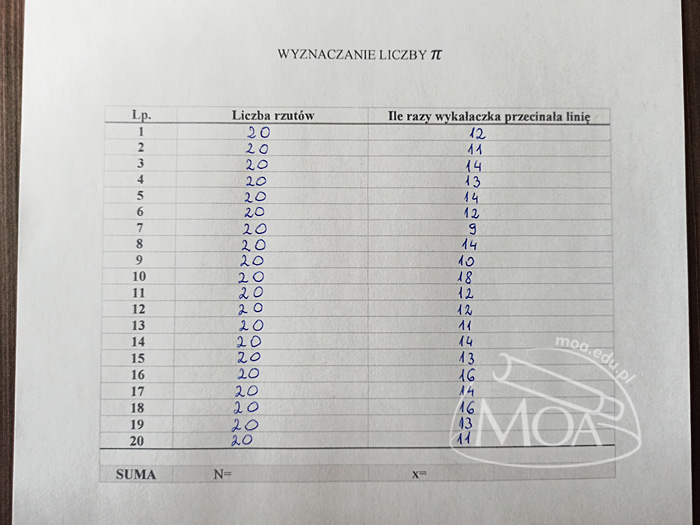
Powtórz czyn­no­ści opi­sa­ne w kro­ku 3. Im wię­cej powtó­rzeń wyko­nasz, tym bliż­szy praw­dzi­wej war­to­ści będzie Twój koń­co­wy wynik. Pro­po­nu­ję, abyś wyko­nał mini­mum 10 powtó­rzeń (czy­li w sumie 200 rzutów).

 

 

KROK 5
Policz ile wyko­na­łeś w sumie rzu­tów oraz ile razy wyka­łacz­ka po rzu­cie prze­ci­na­ła linię.

 

 

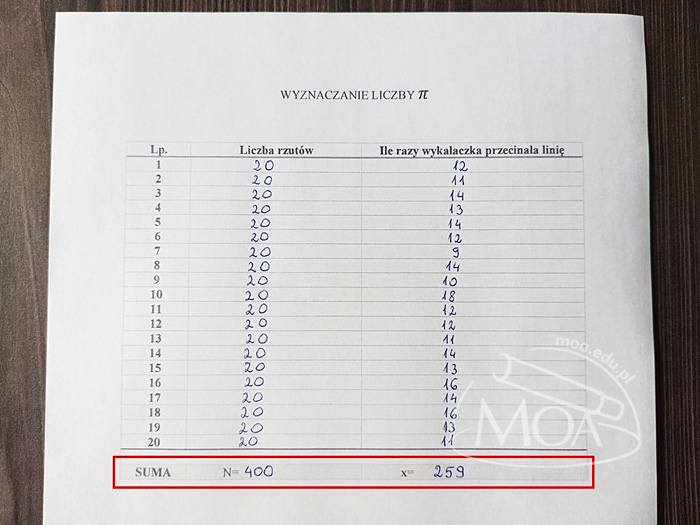
KROK 6
Wyznacz przy­bli­żo­ną war­tość licz­by π korzy­sta­jąc z nastę­pu­ją­ce­go wzoru:

 

 

 

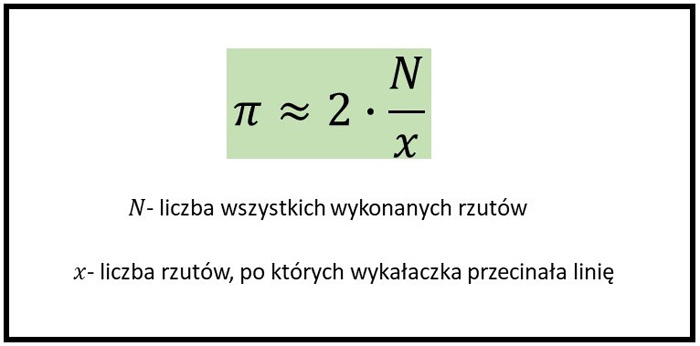
Wyko­na­łam 400 rzu­tów, co pozwo­li­ło mi na osza­co­wa­nie licz­by π jako 3,09. Jest to wynik cał­kiem bli­ski praw­dzi­we­go przy­bli­że­nia licz­by π do dwóch miejsc dzie­sięt­nych, czy­li 3,14. Posta­no­wi­łam spraw­dzić, na ile uzy­ska­na war­tość będzie bliż­sza praw­dy, gdy prze­pro­wa­dzę wię­cej prób.
Zre­ali­zo­wa­łam w sumie 1000 rzu­tów i, ku mojej satys­fak­cji, otrzy­ma­ny rezul­tat wyno­sił w zaokrą­gle­niu 3,14. Aby uzy­ska­ny wynik był zgod­ny z kolej­ny­mi cyfra­mi przy­bli­że­nia dzie­sięt­ne­go licz­by π, nale­ża­ło­by wyko­nać kolej­ne próby.

 

PI JAK PIZZA

Na zakoń­cze­nie zosta­wiam żar­cik mate­ma­tycz­ny zwią­za­ny z licz­bą π:

 

 

Alek­san­dra Kowalska