Zmierz odle­głość do Księżyca

 

Dzi­siaj chcia­łem wam zapro­po­no­wać eks­pe­ry­ment z pomia­rem odle­gło­ści do Księ­ży­ca. Ponie­waż musi­my pozo­stać w domach, potrzeb­ne obra­zy nie­ba wyge­ne­ru­je­my za pomo­cą dar­mo­we­go pro­gra­mu Stel­la­rium (do pobra­nia). Będzie nam też potrzeb­na pod­sta­wo­wa wie­dza z trygonometrii.

„W astro­no­mii para­lak­są nazy­wa się zja­wi­sko pozor­nej zmia­ny poło­że­nia obiek­tu na sfe­rze nie­bie­skiej wzglę­dem dal­szych obiek­tów, wyni­ka­ją­ce ze zmia­ny miej­sca obser­wa­cji, spo­wo­do­wa­nej prze­miesz­cze­niem się obserwatora.”

W naszym przy­pad­ku Księ­życ znaj­du­je się znacz­nie bli­żej Zie­mi niż obe­rwa­ne gwiaz­dy. Jeśli uda nam się zaob­ser­wo­wać jego poło­że­nie na tle gwiazd z dwóch róż­nych miejsc poło­żo­nych na tym samym połu­dni­ku (w tym samym cza­sie), obli­cze­nie odle­gło­ści do nie­go oka­że się cał­kiem łatwe.

Na począ­tek wybierz­my pierw­sze miej­sce obser­wa­cji, dla przy­kła­du ja uży­ję poło­że­nia nasze­go obserwatorium.

 

 

 

Krok 1
Za pomo­cą urzą­dze­nia GPS, tele­fo­nu komór­ko­we­go lub korzy­sta­jąc z ser­wi­su Google Maps ustal poło­że­nie pierw­sze­go miej­sca obserwacji.

Poni­żej przed­sta­wiam jak wyko­nać to za pomo­cą ser­wi­su Google Maps:

Powiększ oko­li­ce miej­sca z któ­re­go pro­wa­dzisz obser­wa­cje lub po pro­stu, w któ­rym miesz­kasz. Następ­nie w wybra­nym miej­scu klik­nij pra­wym kla­wi­szem myszy i wybierz opcję „Co tu jest?”
W dol­nej czę­ści mapy poja­wi się okno zawie­ra­ją­ce współ­rzęd­ne geo­gra­ficz­ne. Zano­tuj je.

 

 

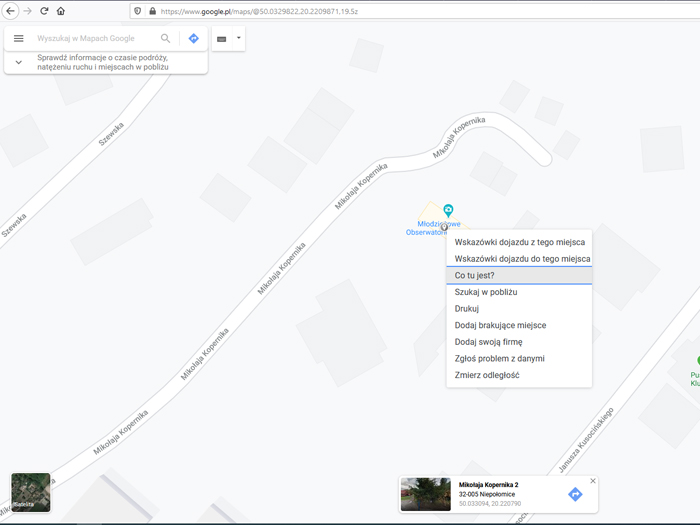
W moim przy­pad­ku to 50.033094N, 20.220790E

 

Krok 2
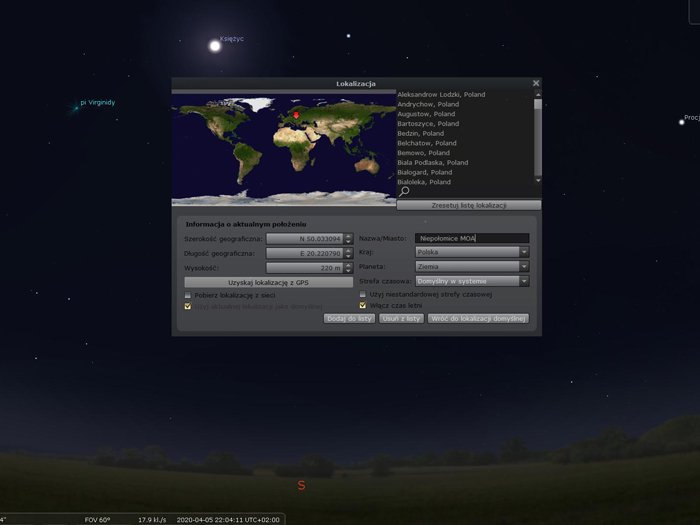
W pro­gra­mie Stel­la­rium wybierz przy­cisk „Okno Loka­li­za­cji” lub wci­śnij kla­wisz F6 na kla­wia­tu­rze. Następ­nie wstaw współ­rzęd­ne uzy­ska­ne w Google Maps lub odczy­ta­ne z GPS.
W polu Nazwa/Miasto wpisz dowol­ną nazwę Loka­li­za­cji. Nie zapo­mnij wci­snąć przy­ci­sku „Dodaj do listy” dzię­ki temu wpi­sa­ne przez Cie­bie dane zosta­ną zapa­mię­ta­ne w programie.
Zamknij okno „Loka­li­za­cja”.

 

 

Krok 3
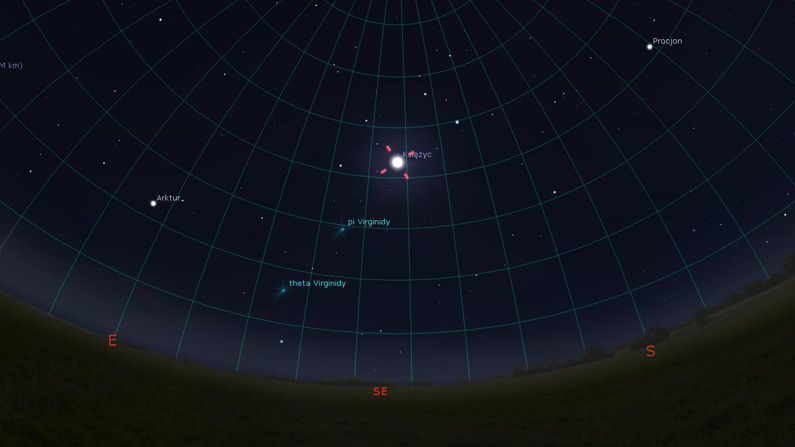
Wyszu­kaj Księ­życ (Okno wyszu­ki­wa­nia – kla­wisz F3).

 

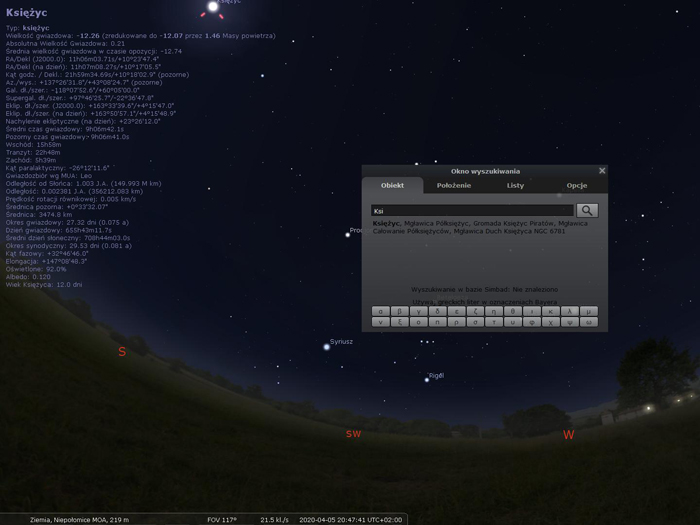
Następ­nie włącz „siat­kę azy­mu­tal­ną” (przy­cisk „Siat­ka azy­mu­tal­na” lub kla­wisz „Z”).

 

 

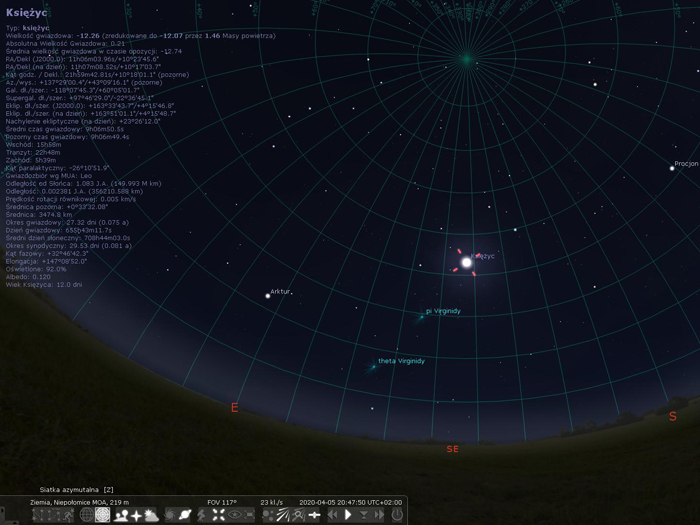
Korzy­sta­jąc z okna „Data i godzi­na” ustaw taki czas, aby Księ­życ był naj­bli­żej linii azy­mu­tu 180 stop­ni (czy­li kie­run­ku połu­dnio­we­go). Możesz tak­że spraw­dzać poło­że­nie Księ­ży­ca w opi­sie po lewej stro­nie (wiersz „Az/wys”). Zatrzy­maj upływ cza­su w pro­gra­mie przy­ci­skiem w menu lub kla­wi­szem „K”.

 

 

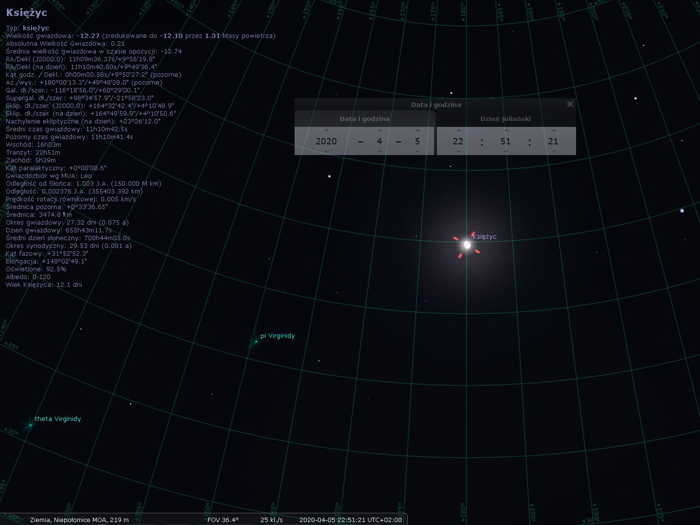
Zano­tuj poło­że­nie Księ­ży­ca (wiersz „Ra/Dekl (na dzień)” w opi­sie Księ­ży­ca) oraz swo­ją lokalizację.

W moim przypadku:

• poło­że­nie Księ­ży­ca: Ra: 11h10m40,8s Dekl: +9º49’36,4”
• loka­li­za­cja (sze­ro­kość i dłu­gość geo­gra­ficz­na): N 50° 1′ 59.13″ E 20° 13′ 14.85″

 

Krok 4
Otwórz ponow­nie okno „Loka­li­za­cja” i zmień sze­ro­kość geo­gra­ficz­ną tak aby Księ­życ zna­lazł się naj­bli­żej zenitu.

 

 

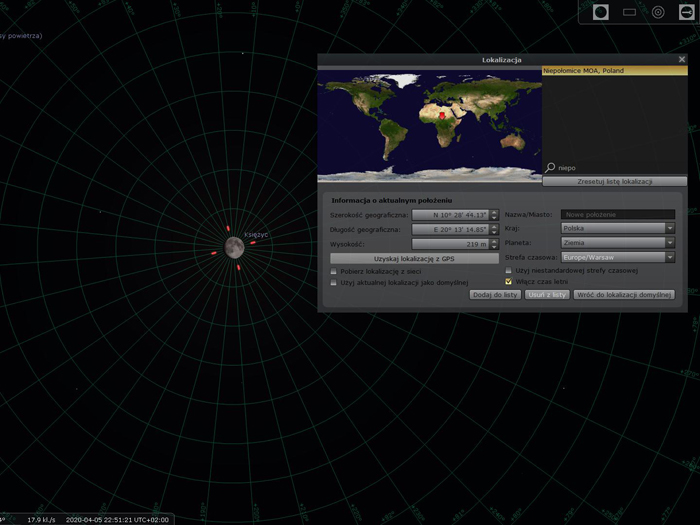
Przyj­rzyj się uważ­nie jak zmie­ni­ło się poło­że­nie Księ­ży­ca wzglę­dem sąsia­du­ją­cych gwiazd.

Zano­tuj ponow­nie poło­że­nie Księ­ży­ca (wiersz „Ra/Dekl (na dzień)” w opi­sie Księ­ży­ca) oraz nową lokalizację.

W moim przy­pad­ku będzie to:

• poło­że­nie Księ­ży­ca na nie­bie (rek­ta­scen­sje i dekli­na­cja): Ra: 11h10m40,8s Dekl: 10º28’44,2”
• loka­li­za­cja (sze­ro­kość i dłu­gość geo­gra­ficz­na): N 10° 28′ 44.13″ E 20° 13′ 14.85″

 

Naszki­cuj­my teraz prze­bieg nasze­go eksperymentu

 

 

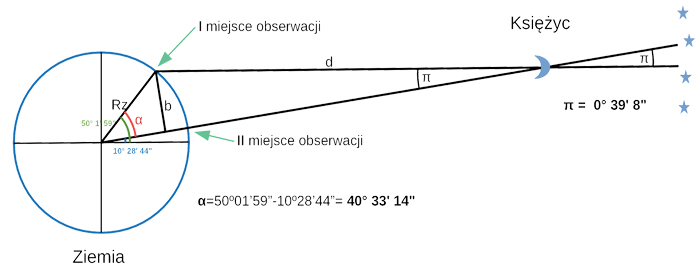
Kąt α uzy­ska­my odej­mu­jąc od sie­bie war­tość sze­ro­ko­ści geo­gra­ficz­nej miejsc obserwacji.

W moim przypadku:
α=50°01’59”-10°28’44”= 40° 33′ 14″

Kąt para­lak­sy π otrzy­ma­my odej­mu­jąc od sie­bie war­tość dekli­na­cji odczy­ta­ną dla obu miejsc obserwacji:

w moim przypadku:
π = 10º28’44” — 9º49’36” = 0º39’08”

aby obli­czyć dłu­gość odcin­ka b sko­rzy­sta­my ze wzo­ru na funk­cję try­go­no­me­trycz­ną sinus:

 

 

 

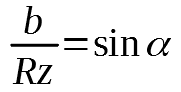
W moim przypadku:

 

 

aby obli­czyć odle­głość od Księ­ży­ca sko­rzy­sta­my z podob­ne­go wzoru:

 

 

 

 

 

 

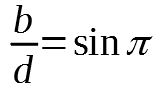
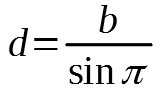
W moim przypadku:

 

 

 

 

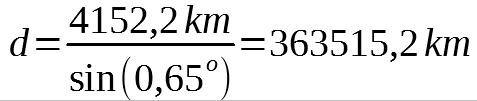
Wynik otrzy­ma­ny to odle­głość pomię­dzy miej­scem obser­wa­cji, a Księżycem.

Nale­ży pamię­tać że odle­głość Zie­mia – Księ­życ nie jest sta­ła, ponie­waż Księ­życ poru­sza się po orbi­cie elip­tycz­nej i waha się od 363 104 km do 405 696 km. Odle­głość, któ­rą więk­szość miło­śni­ków astro­no­mii zna (384400 km), to śred­nia odle­głość do Księżyca.

Życzę wam moż­li­wo­ści prze­pro­wa­dze­nia powyż­sze­go eks­pe­ry­men­tu korzy­sta­jąc z wła­snych obser­wa­cji. Pogod­ne­go nieba !!!

 

Łukasz Maśla­niec